NMR Methodology
(J. Furrer)
a) HMBC Experiments |
b) 1D ROESY |
c) DEPT |
b) 1D ROESY
When the amount of sample available is limited, a series of suitable 1D selective ROESY experiments provide the same information using much less experimental time than the often time consuming 2D ROESY experiment. The setup and the choice of 1D selective ROESY experiments are critical to obtain reliable results. We have proposed a 1D selective ROESY experiment tailor-made for investigating the structure of natural products. The experiment has been tested on a sample of cyclosporine and analyses of the spectra demonstrate that the experiment provides clean spectra allowing reliable cross-peak integration while maintaining high sensitivity. In addition, the experiment does not need a sample-specific setup and can be used as it is starting from standard parameters set by inexperienced users as well as under automated conditions.
-> image 1
For both experiments, thin black bars represent 90° hard pulses, thick bars 180° hard pulses, and shaded half-ellipsis selective 180° pulses. Half-height thick bars represent the phase-alternating 180° pulses of the Tr scheme. Gradient pulses are represented by unfilled half-ellipses denoted by G1 and G2. For diminishing the signal loss due to diffusion, the value of G1 should be around 5 G cm-1. The gradient for eliminating ZQ coherences is represented by a gray bar and denoted G0. δ is the duration of the gradients and the gradient recovery delay. τp is the length of the selective 180° pulse, τm is the mixing time, and n is the number of phase-alternating 180° pulses. The following phase cycle was applied: φ1 = x, -x; φ2 = x, x, y, y, -x, -x, -y, -y; φrec = x, -x, -x, x. This phase cycling leads to substantially better artifact suppression.
-> image 2
image 1: Timing diagrams of the 1D Tr-ROESY (a) and the proposed 1D Tr-GROESY experiment (b) ... full size
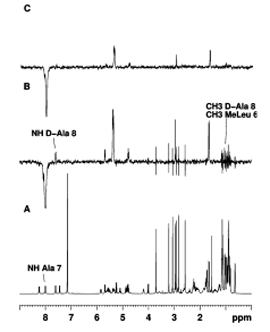
image 2: 1D (a), 1D Tr-ROESY (b), and 1D Tr-GROESY (c) spectra recorded on cyclosporine. The NH
resonance of Ala 7 at 8.00 ppm was selectively inverted using a 50 ms Gaussian pulse.Further Reading
- |
J. Furrer |
- |
D. Jeannerat, J. Furrer |


